2022/02/07
はじめに
いやはや全く困ったものです。
久々にネットで”太いタイヤ”と”グリップ”で検索してみたら、未だに太いタイヤの方がグリップが良いという記事が上位に出てきます。
ちなみに弊サイトのタイヤが太くてもグリップは変わらないとの記事は4番目でした。
それはともかく、太いタイヤの方がグリップが良いとする記事の中に目を惹いたものがあったので、取り上げてみたいと思います。
それはMK RACING(RCが世界を変える。RC1台で工学系学問のすべてが学べる。)なるサイトの以下の記事です。
サイト紹介によれば、管理人は3人でいずれも国立大学もしくは国立大学院卒の様で、リモコンカーに関するサイトと言うのがちと残念ですが、相手にとって不足はありません。
また何故目を惹いたかと言いますと、他のサイトの記事と違ってそれなりに理論的に書かれている様に見えたからです。
おまけに、末尾に参考文献まで記載されているのも好印象です。
さすが国立、しっかり技術文書の書き方を教わっています。
と褒めた所で、早速中身を見ていきたいと思います。
前半
先ずは前半部です。
学生時代、ある友人がこんな疑問を抱きました。「タイムアップする(速く走る)ために太いタイヤを履くことがあるけど、どうして? 物理で習う摩擦力の式には接触面積が登場しないのに…」
実はこの問題、単純な摩擦力の式 F=μN (μ:摩擦係数、N:垂直荷重)では答えのたどり着くことができません。摩擦という現象がどうして発生するのか を考えるとようやく答えを得ることができるのです。いわゆるトライボロジーという学問です。今回は、そのトライボロジーの知見を借りて先述の疑問「タイムアップする(速く走る)ために太いタイヤを履くことがあるけど、どうして?」 を考えてみます。
出だしはまずまずではないでしょうか。
なおトライボロジーとは、ギリシャ語で摩擦という意味です。
だったら摩擦と呼べば良さそうなものですが、トライボロジーとは摩擦と摩耗と潤滑に特化した学問だと思えば大きな間違いではないでしょう。
これを含めて前半は、しっかりタイヤのグリップは接触面積には関係ないと述べています。
とは言いながら、そもそも速く走るために太いタイヤを履くこと自体が大間違いなのですが、ここでは取り敢えず先に進みます。
このチャートは本物か?
そして中盤になると、いよいよこのトライボロジーの話と下のチャートが出てきます。
ここからが重要です。荷重と摩擦力関係を今までの知識F=μNで考えると、荷重が大きくなると摩擦力もいくらでも大きくなるのですが、“実際”はそうならないのです。 実際には以下の図の赤線のように荷重が大きい場合、荷重と摩擦力は比例関係ではなくなります。つまり荷重が増加しても摩擦力は大きくならなくなります。
どうやら摩擦力はF=μNの様にリニアに増えていくのに対して、トライボロジーにおいては、右のチャートの様にF=μNの関係が成り立たなくなると言いたい様です。
確かにそれは有り得るかもしれません。
例えばゴム片にとてつもない荷重を加えれば、もうゴムと呼べる様な物ではなく、カチカチの物体になるので、さすがに摩擦力はリニアに増えない様な気もします。
そしてこれより更に荷重を加えると、いつかゴムが破裂するのでしょう。
ご存知かもしれませんが、下は金属の応力歪曲線です。
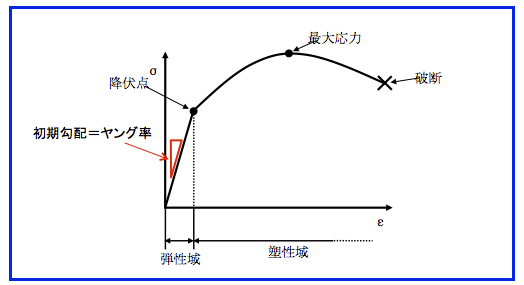
金属の応力歪曲線
先ほどのチャートと、かなり似た様なカーブではないでしょうか。
これは金属棒を引っ張るとしばらくはリニアに延びて、且つ力を抜くと元に戻るものの(弾性域)、降伏点を過ぎるとその特性は失われて変形し(塑性域)、さらに力を加えると最後は破断するというものです。
なぜいきなりこんな図を持ち出したかと言えば、金属をバネとして使う場合は、当然ながら降伏点より下の応力域で使う事になります。
そうでなければ、バネが潰れてしまうか、延びてしまって、バネの役目を果たせなくなるからです。
すなわち工業製品であれば、ゴム(タイヤ)でも金属(バネ)でもその目的に応じた領域を使う様にしているという事です。
故にF=μNの関係が成り立たなくなる条件で、ゴムを使うなんて非常識な事をする訳がありません。
と、ここまで書いていてアレッ?と疑問が頭を横切りました。
先ほど金属の応力歪曲線は、それなりの試験機がいくらでも存在しています。

実際万力の様に、金属を両方から強い力で引っ張るのは比較的容易にできます。
ところが摩擦力の測定においては、サンプルに荷重を掛けた状態で、更にサンプルを横にずらさなければなりません。
そんな試験機は存在するのでしょうか?
そんな訳で急遽この記事の参考文献である、はじめてのトライボロジー(講談社)を取り寄せて調べてみました。
すると、こんなチャートはどこにも出てこないのです。
このチャートはどこから持ってきたのでしょう?
もし存在しないチャートを想像で描いたとしたら、この記事は間違いなく捏造記事です。
添付チャートの問題点
そう思うと、このチャートの幼稚さも納得できます。
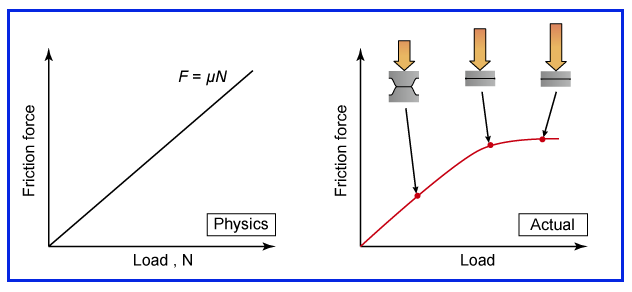
先ず左側の図は、直線の上にF=μNと書いてあるので摩擦力と抗力の関係を表すチャートなのでしょう。
にも関わらず、横軸(X軸)はLoad, Nとなっています。
この式(F=μN)のNとは、Normal Force(垂直抗力)を表しているので、横軸はNormal ForceもしくはFnと記入すべきです。
また縦軸にFriction Forceとありますが、PhysicsにおいてFrictionは力の意味が含まれていますので、正しくはFrictionと書くべきです。
これらは多少許せても、頂けないのがPhysics(物理)とActual(現実の)です。
恐らくこの図で言いたいのは、左は物理の教科書にある建前で、右が現実だとでも言いたいのでしょう。
ですが仮に右のチャートが本物だとしても、切り出す部分が違うだけで、いずれも現実なのです。
ついでに言わせて頂ければ、Actualとは形容詞ですので、本来ならばこの後に何らかの名詞が続かなければなりません。
そして致命的なのは、このチャートにタイトルが書かれていない事です。
技術論文の添付図には、必ずタイトルなりキャプションを入れなければなりません。
ネットの記事とは言え、本当に国大卒かなと徐々に疑いが湧いてきました。
説明とチャートが全く合っていない
かなり怪しいチャートですが、(無い事の証明はできないので)取り敢えずこれは本物だという事で話を進めます。
で、下の記述をジックリ読んで頂けますでしょうか。
いよいろ本題、速く走るため太タイヤを履く理由を考えます。
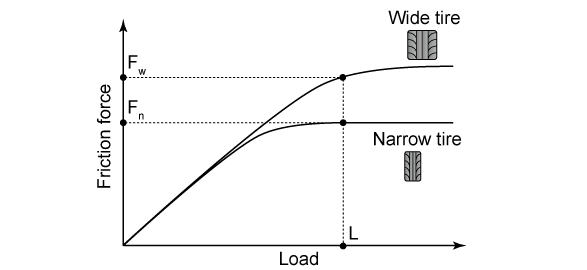
結論から言うと「タイヤ幅を太くして、荷重と摩擦力が比例関係を保つ荷重領域を増やすことでグリップの限界が上がるから」です。
下図に細いタイヤと太いタイヤの荷重と摩擦力の関係を模式的に示します。荷重と摩擦力が関係を失う荷重を限界荷重と呼ぶことにすると、細いタイヤの限界荷重より太いタイヤの限界荷重の方が 大きくなります。
そしてこの文章とこのチャートの根本的な間違いに気付いて頂けましたでしょうか?
文面では、”荷重と摩擦力が比例関係を保つ荷重領域を増やすことでグリップの限界が上がるから”とありながら、下のチャートでは荷重は同じ所を指しているのです。
何だこりゃ、と言った感じです。
おまけに、いきなり太いタイヤと細いタイヤの異なる曲線が出てきますが、その根拠は何なのでしょうか?
その説明は一切書かれていません。
まとめ
そんな訳で、この記事は出所不明のチャートを元に書かれている可能性が非常に高く、おまけにそのチャートはかなり幼稚な出来で、さらに肝心な結論部分の説明と説明図が合っていないといった、非常にお粗末な物と言わざるを得ません。
大人になってラジコンで遊ぶのは悪い事ではないのですが、国大卒の3人が管理しているサイトとは、正直思えません。